1) Sketch the parabola, and lable the focus, vertex and directrix. a) (y - 1)^2 = -12(x + 4) b) i) y^2 - 6y -2x + 1 = 0, ii) y =
Por um escritor misterioso
Last updated 23 dezembro 2024


Day 18 Warm-Up 1) Which of the following problems is a circle and which is a parabola? Why? A) ppt download
parabola generator: vertex, focus, directrix
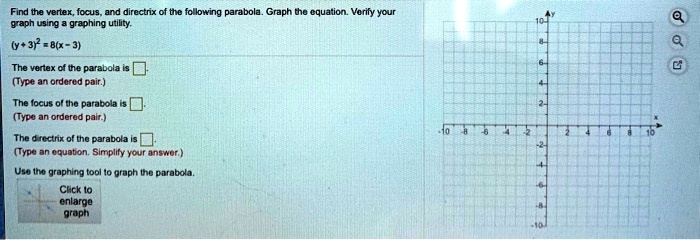
SOLVED: Find the vertex, focus, and directrix of the following parabola. Graph the equation using a graphing tool. (y + 3)^2 = 8(x - 2) The vertex of the parabola is (2,

Consider the sketch of the parabola. Let $p$ represent the d
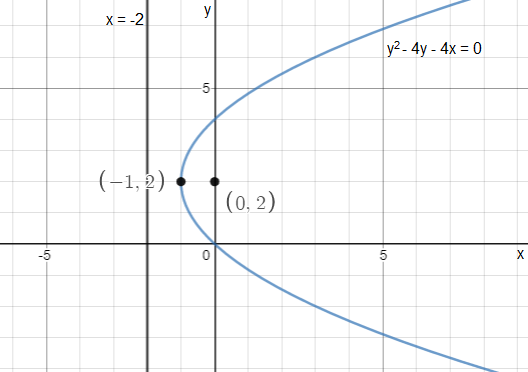
Find the vertex, focus, and directrix of the parabola, and s
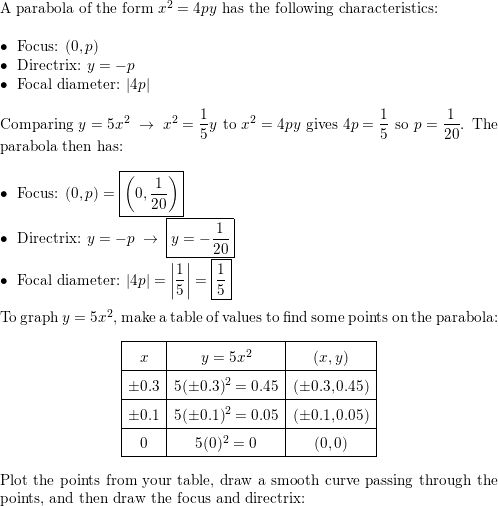
Find the focus, directrix, and focal diameter of the parabol

Conic sections: Analyzing Conic Sections with the Algebraic Method - FasterCapital
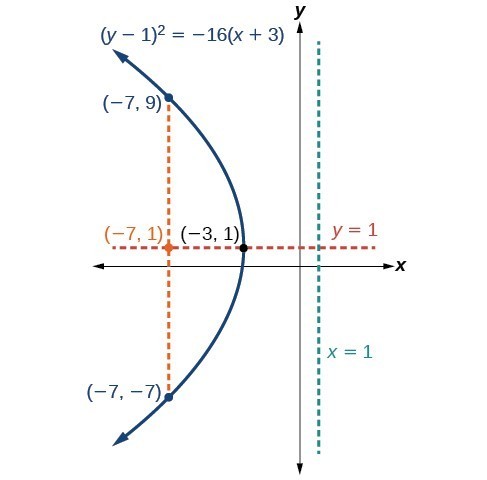
Graphing Parabolas with Vertices Not at the Origin, College Algebra

geometry - Focus of parabola with two tangents - Mathematics Stack Exchange

Pre-Calculus Prep: Conic Sections - Graph the Ellipse

Conic sections: Analyzing Conic Sections with the Algebraic Method - FasterCapital
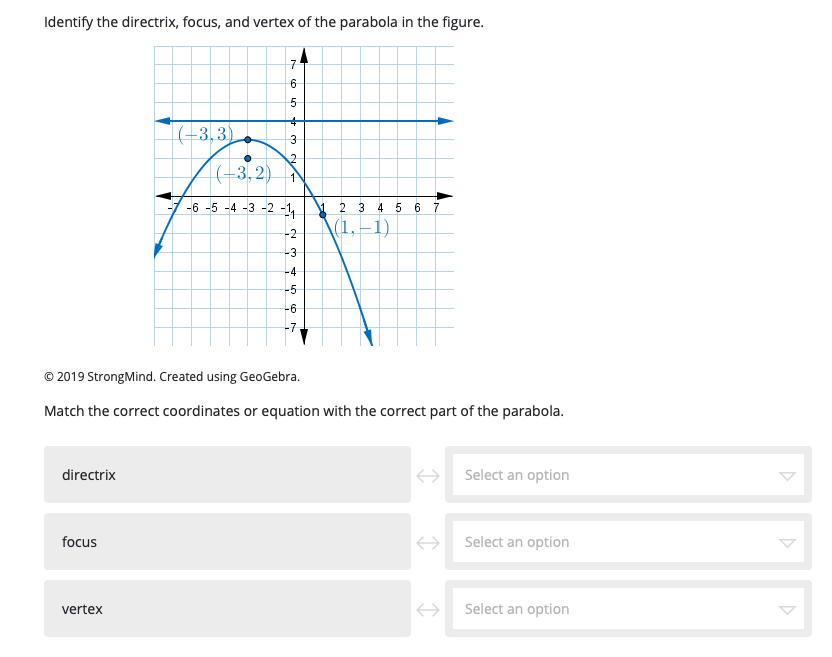
Answered: Identify the directrix, focus, and…

SOLVED: Use the given equation to identify the direction the parabola is opening, and the vertex, focus, and directrix for the parabola. Then, graph the parabola. Include the focus, vertex, directrix, and
Solved] I. Find the center, vertices, foci, ends of the latera recta and
Recomendado para você
-
![SOLVED] Download DirectX 12 for Windows 10 - Driver Easy](https://images.drivereasy.com/wp-content/uploads/2018/11/Snap630.png) SOLVED] Download DirectX 12 for Windows 10 - Driver Easy23 dezembro 2024
SOLVED] Download DirectX 12 for Windows 10 - Driver Easy23 dezembro 2024 -
 DirectX 12 - Download for PC Free23 dezembro 2024
DirectX 12 - Download for PC Free23 dezembro 2024 -
 Baixar e Instalar a DirectX 1223 dezembro 2024
Baixar e Instalar a DirectX 1223 dezembro 2024 -
 DirectX 12 Download For Windows 10, 8, 7, XP 64 Bit / 32 Bit23 dezembro 2024
DirectX 12 Download For Windows 10, 8, 7, XP 64 Bit / 32 Bit23 dezembro 2024 -
Directx 9.0C Compatible 3D Accelerated 64Mb Video Card Download - Colaboratory23 dezembro 2024
-
DirectX - Wikipedia23 dezembro 2024
-
 Warframe DX11 vs DX12 Round 2 Update 29.6.3 (no GPU bound)23 dezembro 2024
Warframe DX11 vs DX12 Round 2 Update 29.6.3 (no GPU bound)23 dezembro 2024 -
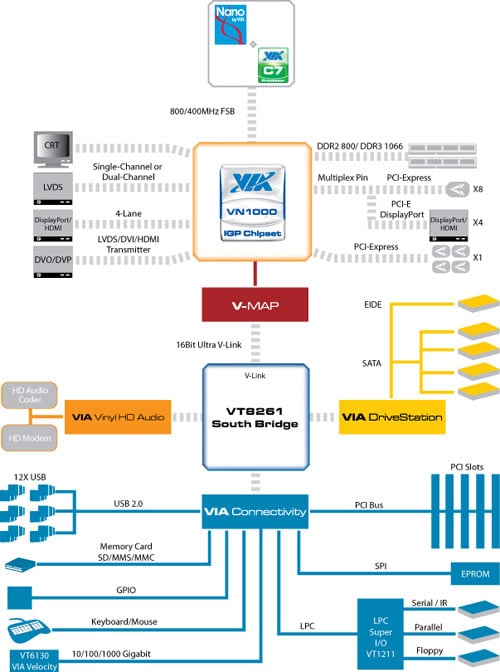 VIA Announces VN1000 Power Efficient DX10.1 Chipset23 dezembro 2024
VIA Announces VN1000 Power Efficient DX10.1 Chipset23 dezembro 2024 -
 Timescape: Journey to Pompeii Box Shot for PC - GameFAQs23 dezembro 2024
Timescape: Journey to Pompeii Box Shot for PC - GameFAQs23 dezembro 2024 -
 Placa de Vídeo JieShuo Radeon RX 6600 XT, 8GB, GDDR6, 128-Bit, Nova ou 12X 144,30 - Computadores e acessórios - Vila Marumby, Maringá 123317347623 dezembro 2024
Placa de Vídeo JieShuo Radeon RX 6600 XT, 8GB, GDDR6, 128-Bit, Nova ou 12X 144,30 - Computadores e acessórios - Vila Marumby, Maringá 123317347623 dezembro 2024
você pode gostar
-
 Gardevoir V - SWSH10523 dezembro 2024
Gardevoir V - SWSH10523 dezembro 2024 -
 FNAF Security Breach Animatronics Size Comparison Five Nights at Freddy's Character Heights23 dezembro 2024
FNAF Security Breach Animatronics Size Comparison Five Nights at Freddy's Character Heights23 dezembro 2024 -
 Wimbledon day one23 dezembro 2024
Wimbledon day one23 dezembro 2024 -
 How to Set Ratings (FIDE and USCF) for Students?23 dezembro 2024
How to Set Ratings (FIDE and USCF) for Students?23 dezembro 2024 -
 Fun Math Games to Play with Uno Cards23 dezembro 2024
Fun Math Games to Play with Uno Cards23 dezembro 2024 -
BEST 5 LOW END PC GAMES 2022, LOW SPECS PC GAMES, 2GB RAM PC GAMES NO GRAPHICS CARD, a to zvideos, government, personal computer, random-access memory23 dezembro 2024
-
 Sword Art Online Alternative: Gun Gale Online Episode 3: Fan Letter Review - IGN23 dezembro 2024
Sword Art Online Alternative: Gun Gale Online Episode 3: Fan Letter Review - IGN23 dezembro 2024 -
 Shillelaghs and Shenanigans 2 - Combat Shillelagh23 dezembro 2024
Shillelaghs and Shenanigans 2 - Combat Shillelagh23 dezembro 2024 -
 LEGO Batman: The Movie - DC Super Heroes Unite, Full Movie23 dezembro 2024
LEGO Batman: The Movie - DC Super Heroes Unite, Full Movie23 dezembro 2024 -
 Tourists on Fisherman`s Wharf, Pier 39 at Carousel Editorial Stock23 dezembro 2024
Tourists on Fisherman`s Wharf, Pier 39 at Carousel Editorial Stock23 dezembro 2024
