Casastrangers to friends

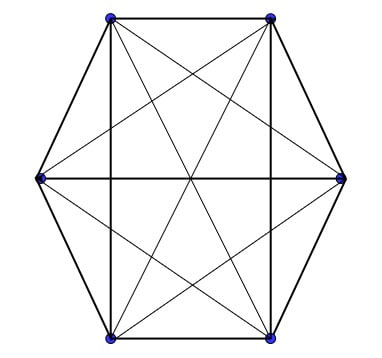
Theorem on Friends and Strangers; Why in Any Party of Six People, Either at Least Three of Them Are Mutual Friends, or at Least Three of Them Are Mutual Strangers

Por um escritor misterioso
Last updated 11 novembro 2024
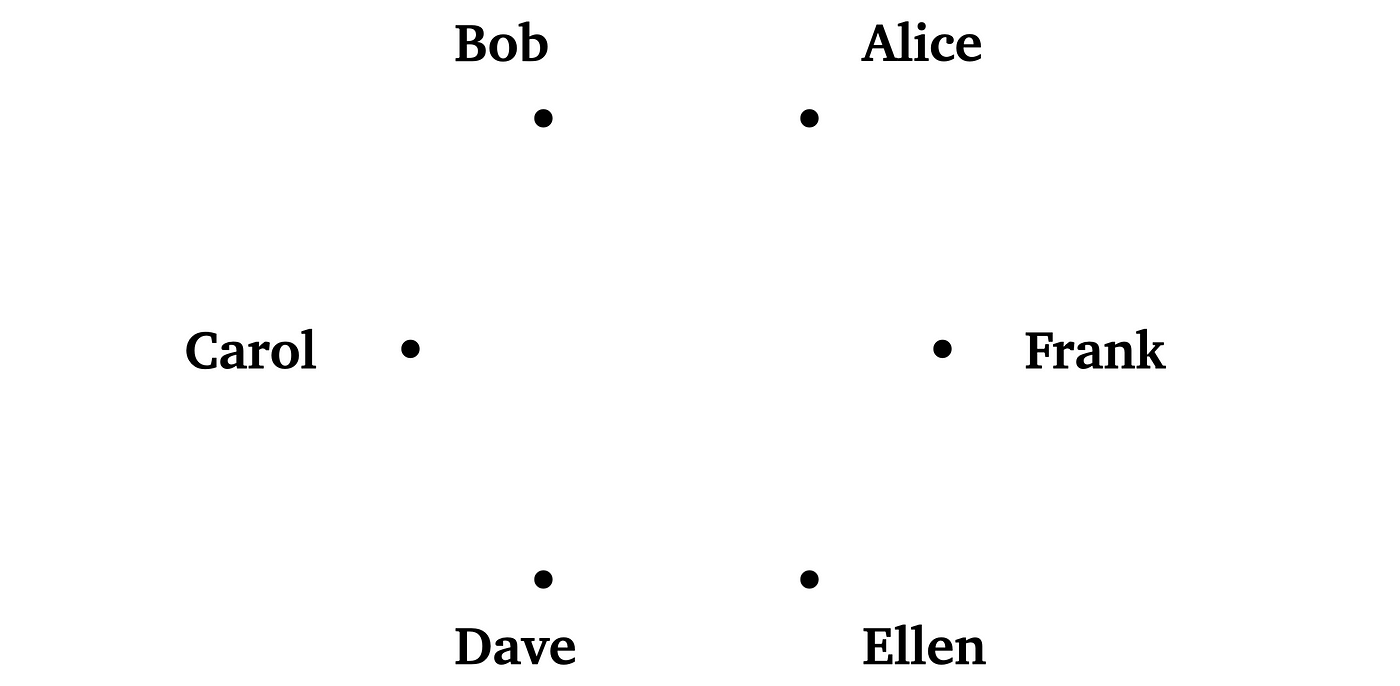
Theorem on Friends and Strangers; Why in Any Party of Six People, Either at Least Three of Them Are Mutual Friends, or at Least Three of Them Are Mutual Strangers
Let’s take a look at Alice first. To her, each one of the other five (Bob, Carol, Dave, Ellen, and Frank) is either a friend or a stranger. Suppose Bob, Dave, and Frank are friends to Alice, and…
Theorem on Friends and Strangers; Why in Any Party of Six People, Either at Least Three of Them Are Mutual Friends, or at Least Three of Them Are Mutual Strangers
Friends and strangers
Theorem on Friends and Strangers; Why in Any Party of Six People, Either at Least Three of Them Are Mutual Friends, or at Least Three of Them Are Mutual Strangers
Party At Ramsey's
Theorem on Friends and Strangers; Why in Any Party of Six People, Either at Least Three of Them Are Mutual Friends, or at Least Three of Them Are Mutual Strangers
Correlation, Causation, and Ramsey Theory
Theorem on Friends and Strangers; Why in Any Party of Six People, Either at Least Three of Them Are Mutual Friends, or at Least Three of Them Are Mutual Strangers
Solved Show that in a group of five people (where any two
Theorem on Friends and Strangers; Why in Any Party of Six People, Either at Least Three of Them Are Mutual Friends, or at Least Three of Them Are Mutual Strangers
Can Math Prove You'll Always Be the Odd One Out At Parties?, by Mary Paskhaver, Geek Culture
Theorem on Friends and Strangers; Why in Any Party of Six People, Either at Least Three of Them Are Mutual Friends, or at Least Three of Them Are Mutual Strangers
Ramsey Theory on Facebook - Scientific American Blog Network
Theorem on Friends and Strangers; Why in Any Party of Six People, Either at Least Three of Them Are Mutual Friends, or at Least Three of Them Are Mutual Strangers
Madeline Dawsey--Modular Forms and Ramsey Theory.
Theorem on Friends and Strangers; Why in Any Party of Six People, Either at Least Three of Them Are Mutual Friends, or at Least Three of Them Are Mutual Strangers
Theorem on Friends and Strangers. Ramsey Theory and Graham's Number, by Francesco Di Lallo
Theorem on Friends and Strangers; Why in Any Party of Six People, Either at Least Three of Them Are Mutual Friends, or at Least Three of Them Are Mutual Strangers
How to prove: at a party of six people either there are three mutual acquaintances or there are three mutual strangers - Quora
Theorem on Friends and Strangers; Why in Any Party of Six People, Either at Least Three of Them Are Mutual Friends, or at Least Three of Them Are Mutual Strangers
How Math Puzzles Help You Plan the Perfect Party
Theorem on Friends and Strangers; Why in Any Party of Six People, Either at Least Three of Them Are Mutual Friends, or at Least Three of Them Are Mutual Strangers
The Ramsey Theory Baeldung on Computer Science
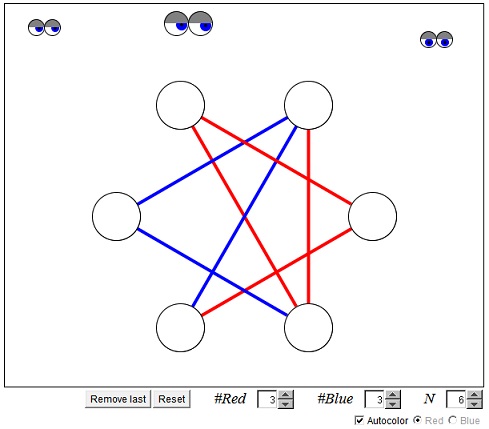
Theorem on Friends and Strangers; Why in Any Party of Six People, Either at Least Three of Them Are Mutual Friends, or at Least Three of Them Are Mutual Strangers
Party Acquaintances
Theorem on Friends and Strangers; Why in Any Party of Six People, Either at Least Three of Them Are Mutual Friends, or at Least Three of Them Are Mutual Strangers
Party Problem The simplest example of Ramsey theory. It is also known as the 'Maximum Clique Problem'. A clique of a graph is a complete sub graph of the. - ppt download
Recomendado para você
você pode gostar

© 2014-2024 immanuelipc.com. All rights reserved.