Lecture 15: Steepest Descent Method for Asymptotic Analysis (Chapter 15) - Lectures on Random Lozenge Tilings
Por um escritor misterioso
Last updated 31 dezembro 2024


Steepest descent least-squares optimisation - derivation explained (watch before conjugate gradient)

Steepest Descent Method - an overview

Doubly periodic lozenge tilings of a hexagon and matrix valued orthogonal polynomials - Charlier - 2021 - Studies in Applied Mathematics - Wiley Online Library

Steepest Descent Method

Skew Howe duality and limit shapes of Young diagrams - Nazarov - Journal of the London Mathematical Society - Wiley Online Library

Lectures on Random Lozenge Tilings
JGAAP/src/com/jgaap/resources/ELPrt.dat at master · evllabs/JGAAP · GitHub

Lecture 4: Counting Tilings on a Large Torus (Chapter 4) - Lectures on Random Lozenge Tilings

Lecture 20: GUE-Corners Process and Its Discrete Analogues (Chapter 20) - Lectures on Random Lozenge Tilings

PDF) A Periodic Hexagon Tiling Model and Non-Hermitian Orthogonal Polynomials

The Steepest-Descent Method - ppt video online download
Recomendado para você
-
 Steepest Descent Method - an overview31 dezembro 2024
Steepest Descent Method - an overview31 dezembro 2024 -
 Steepest Descent and Newton's Method in Python, from Scratch: A Comparison, by Nicolo Cosimo Albanese31 dezembro 2024
Steepest Descent and Newton's Method in Python, from Scratch: A Comparison, by Nicolo Cosimo Albanese31 dezembro 2024 -
 Steepest descent method31 dezembro 2024
Steepest descent method31 dezembro 2024 -
 MATLAB script file implementing the method of steepest descent31 dezembro 2024
MATLAB script file implementing the method of steepest descent31 dezembro 2024 -
 7: An example of steepest descent optimization steps.31 dezembro 2024
7: An example of steepest descent optimization steps.31 dezembro 2024 -
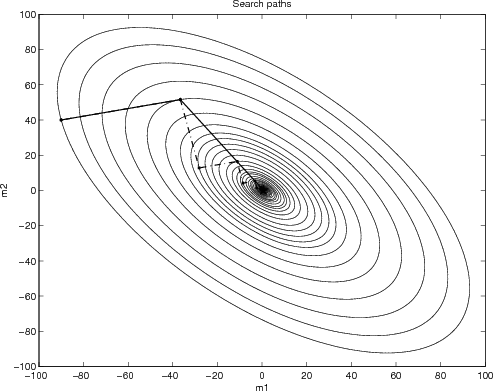 Why steepest descent is so slow31 dezembro 2024
Why steepest descent is so slow31 dezembro 2024 -
 Using the Gradient Descent Algorithm in Machine Learning, by Manish Tongia31 dezembro 2024
Using the Gradient Descent Algorithm in Machine Learning, by Manish Tongia31 dezembro 2024 -
 example of steepest Descent (left) and Conjugate Gradient (right)31 dezembro 2024
example of steepest Descent (left) and Conjugate Gradient (right)31 dezembro 2024 -
 PDF) Steepest Descent juan meza31 dezembro 2024
PDF) Steepest Descent juan meza31 dezembro 2024 -
 Solved The steepest descent method for minimize f(x) is the31 dezembro 2024
Solved The steepest descent method for minimize f(x) is the31 dezembro 2024
você pode gostar
-
 10 Motivos pra Você Começar a Assistir Hora de Aventura Agora Mesmo, by Matheus Ferreirinha, Água de Salsicha31 dezembro 2024
10 Motivos pra Você Começar a Assistir Hora de Aventura Agora Mesmo, by Matheus Ferreirinha, Água de Salsicha31 dezembro 2024 -
 Vale-Presente FREE FIRE GOOGLE PLAY: ASSINATURA MENSAL - GCM Games31 dezembro 2024
Vale-Presente FREE FIRE GOOGLE PLAY: ASSINATURA MENSAL - GCM Games31 dezembro 2024 -
 But hey that's just a theory, AN SCP THEORY. - Imgflip31 dezembro 2024
But hey that's just a theory, AN SCP THEORY. - Imgflip31 dezembro 2024 -
 Anime Streaming News HIDIVE for December 202331 dezembro 2024
Anime Streaming News HIDIVE for December 202331 dezembro 2024 -
 Movie review: My Little Pony31 dezembro 2024
Movie review: My Little Pony31 dezembro 2024 -
 Assistir Death Note Dublado - Episódio - 1 animes online31 dezembro 2024
Assistir Death Note Dublado - Episódio - 1 animes online31 dezembro 2024 -
 10 Receitas de bolo simples para o café da tarde31 dezembro 2024
10 Receitas de bolo simples para o café da tarde31 dezembro 2024 -
Centro Britânico Idiomas - Santana31 dezembro 2024
-
 Jogos de skate gerados por ai31 dezembro 2024
Jogos de skate gerados por ai31 dezembro 2024 -
 Preço do PlayStation Plus de 12 meses vai aumentar em Setembro31 dezembro 2024
Preço do PlayStation Plus de 12 meses vai aumentar em Setembro31 dezembro 2024
